INTRODUCTION

La conception de la structure pour l’analyse dynamique implique la création d’un modèle de calcul qui reflète fidèlement le comportement dynamique réel de la structure ; dans ce processus, l’expérience et le discernement du calculateur jouent un rôle crucial. Même pour des structures qui semblent simples en apparence, une modélisation efficace requiert généralement une série de réflexions et de décisions concernant les aspects suivants :

• Dans le cas des ouvrages qui présentent une dissymétrie pour lesquels l’excitation est hors de leur plan, il faut considérer une modélisation tridimensionnelle.
• Déterminer le degré de précision souhaité par le modèle : résultats détaillés des sollicitations ou simplement une réponse globale.
• Définir les propriétés mécaniques des matériaux utilisés
• Définition approprié des degrés de liberté dynamique de l’ouvrage
• Définition approprié des rigidités des éléments de l’ouvrage
• Définition approprié des valeurs de l’amortissement à adopter

La répartition des raideurs et des masses de l’ouvrage découle d’une bonne modélisation du pont et d’un choix approprier des degrés de liberté dynamique.

Ainsi, lors de l’application de l’excitation sismique de calcul, la mobilisation des modes de déformations et des forces d’inertie de l’ouvrage est complète.

En général, deux modèles d’analyse sont adoptés, le premier modèle correspond à une modélisation du comportement du pont longitudinalement, le second s’attèle à une modélisation du comportement du pont transversalement.

Concernant l’estimation des masses, il faut considérer la valeur moyenne des masses des actions permanentes, plus les valeurs moyennes des masses des actions variables.

Suivant le degré de liberté choisis, les masses réparties peuvent être prise concentrées aux nœuds.

Pour dimensionner, les valeurs moyennes des charges permanentes sont identifiées par leurs valeurs caractéristiques ; les valeurs quasi-permanentes des charges variables sont représentées par ψ21 Q1K.

Ou Q1K est la valeur caractéristique de la charge due au trafic :

Pour les ponts supportant un trafic inportant, Les valeurs recommandées de ψ12 sont les suivantes : – Ponts-routes ψ12 = [0,2] ; – Ponts-rails ψ12 = [0,3] ;

Lorsque les piles sont immergées dans l’eau, en l’absence d’une approche rigoureuse de l’interaction hydrodynamique, cet effet peut être estimé en considérant une masse additionnelle d’eau déplacée par unité de longueur des piles immergées.

RIGIDITES DES ELEMENTS

 Rigidité des appareils d’appuis en élastomère frettés

La relation suivante exprime la rigidité d’un dispositif d’appui en élastomère fretté de dimensions a x b x e :

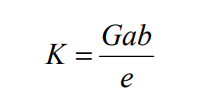
Avec G : le module de cisaillement de l’appareil d’appui

En l’absence de tests spécifiques, le guide AFPS 92 recommande de sélectionner le module de cisaillement dans une plage comprise entre 0,8 et 1,2 MPa.

Nous choisirons la valeur maximale G = 1,2 MPa, correspondant aux charges maximales.

 Rigidité des piles

Le calcul des rigidités des piles intègre les rigidités élastiques avant fissuration, incluant les inerties de coffrage, afin d’obtenir un modèle qui est sensiblement plus rigide que la structure réelle, assurant ainsi la sécurité des charges.

La raideur Ki d’une ligne d’appui est définie par :

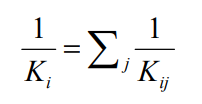
Ou Kij est la raideur d’une partie j (fut ou appareil d’appuis) de l’appui i

-Pour un fut de pile bloqué en tête, caractérisé par sa hauteur hpile, son inertie de coffrage Ipile et son module instantané Ebéton, et avec un appareil d’appui fixe, la rigidité de la pile est déterminée par :

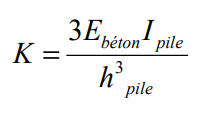
-Pour un appui équipé de n appareils d’appui en élastomère de dimensions horizontales a x b et d’épaisseur e, la rigidité est la combinaison en série de la rigidité du fut et de la rigidité des appareils d’appui.

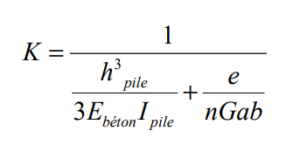
– pour un fut encastré en tête et en pied :

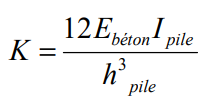
AMORTISSEMENT

Conventionnellement, l’amortissement dans un matériau est représenté par un modèle visqueux. Le taux d’amortissement critique ζ (en %) varie comme suit :

Matériau	Taux d’amortissement en %
Acier soudé	2
Acier boulonné	4
Béton précontraint	2
Béton non armé	3
Béton armé	5
Élastomère fretté	7

Pour les structures où les modes propres impliquent la déformation simultanée d’éléments fabriqués à partir de matériaux différents, on sélectionne l’amortissement le plus bas ou on effectue le calcul d’un amortissement moyen pour chaque mode.

Lorsqu’un pont est équipé de dispositifs amortisseurs, il est important de noter que :

• Ces dispositifs agissent souvent comme un système combinant ressort et amortisseur en parallèle. Il est nécessaire de calculer leur rigidité et de l’intégrer au modèle d’analyse.
• Les dispositifs amortisseurs sont généralement associés à un coefficient d’amortissement d’une valeur très élevée, ce qui peut entraîner une matrice d’amortissement du système divergeant considérablement du cas diagonalisé basé sur les modes propres non amortis. Il est essentiel de prendre en compte ce choix lors de la sélection de la méthode de résolution. Pour les structures où les éléments déformables sont fabriqués à partir de matériaux différents, le calcul de l’amortissement moyen d’un mode peut être effectué selon la formule suivante :

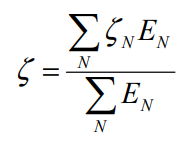
Dans laquelle :

– EN désigne l’énergie de déformation élastique de la liaison n° N dans la déformée du mode considéré;

– ζN désigne l’amortissement du matériau constitutif de la liaison n°N.

MODELISATION

Pour les ouvrages standards, la flexibilité des fondations est généralement ignorée lors de la justification du tablier et des appuis en élévation. Cela entraîne une augmentation de la rigidité globale de l’appui et donc une diminution de la période naturelle de l’ouvrage. Les charges sont ainsi généralement surestimées, ce qui garantit une marge de sécurité. Cependant, les déplacements sont souvent sous-estimés. En revanche, pour un tablier reposant sur des élastomères frettés ou des appuis glissants, il est essentiel de calculer les déplacements du tablier afin de dimensionner les longueurs des appuis et des butées parasismiques. Dans ce cas, la flexibilité des fondations a peu d’impact sur la période naturelle de l’ouvrage, permettant ainsi de calculer correctement les déplacements du tablier en négligeant cette flexibilité. Cependant, l’interaction entre le sol et les pieux peut être cruciale pour le calcul statistique équivalent des sollicitations dans les pieux. Les modules élastiques dynamiques des sols (qui diffèrent considérablement des valeurs issues des essais pressiométriques classiques) et les caractéristiques de la liaison sol-pieu sont déterminés de la manière suivante :

Evaluation des caractéristiques du sol

Les normes spécifient que les propriétés du sol doivent être déterminées à partir d’un ensemble d’essais appropriés. Ces essais fournissent généralement la valeur de la vitesse maximale des ondes de cisaillement Vs,max (pour de petites perturbations) dans les différentes couches de sol concernées par la fondation. À partir de ces vitesses, le module de cisaillement Gmax est obtenu en utilisant la formule suivante :

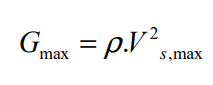
Ou ρ est la masse volumique de la couche de sol

Détermination des raideurs de sol

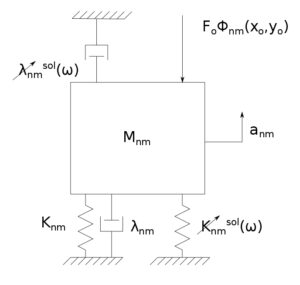
Les fondations superficielles : Pour ces dernières, les raideurs peuvent être déterminées en considérant des fréquences nulles (approche pseudo-élastique), pour une fondation circulaire équivalente s’appuyant sur un demi-espace élastique.

– Fondation réelle  

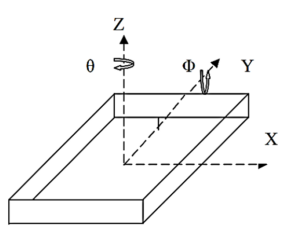
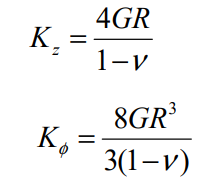
-Fondation circulaire équivalente

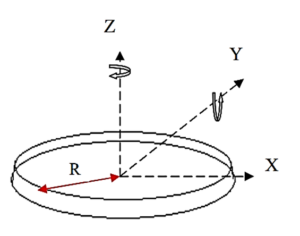
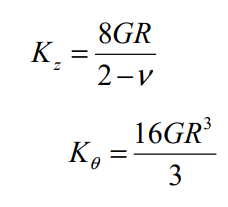
Les pieux : La raideur horizontale du sol par mètre linéaire de pieu reste constante et ne dépend pas du diamètre du pieu.

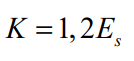
Avec

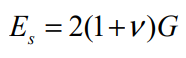
Dans le cas où des informations plus précises ne sont pas disponibles, le coefficient de Poisson du sol (ν) est pris égal à 0,3, et G représente le module de cisaillement.